This program uses the Gregory-Leibniz series for calculating the value of PI. Note that this series is slow and there exist other faster algorithms for calculating the value of PI.
A simple infinite series for π is the Gregory–Leibniz series:
A simple infinite series for π is the Gregory–Leibniz series:
As individual terms of this infinite series are added to the sum, the total gradually gets closer to π, and – with a sufficient number of terms – can get as close to π as desired. It converges quite slowly, though – after 500,000 terms, it produces only five correct decimal digits of π.
Source:
public class PI {
static float calculate() {
float denom = 1, sum = 0, numerator = -4.0f;
for(int i=0;i<500000;++i){
float nextTerm = (numerator=-numerator) / (denom);
sum += nextTerm;
denom+=2;
}
return sum;
}
public static void main(String[] args) {
System.out.println(calculate());
}
}
Output:
3.141594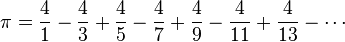
No comments:
Post a Comment